Maximum Score from Performing Multiplication Operations

Tagged: Array, Dynamic Programming

Problem#

We are given two array of integers nums and multipliers of size n and m respectively, where n >= m.

Begin with a score of 0, we want to perform exactly m operations. On the i^th operation, we will:

• Choose an integer x from either the start or the end of the array nums.
• Add multipliers[i] * x to your score.
• Remove x from the array nums.

Our task is to find the maximum score after performing m operations.

For example,

Input: nums = [1,2,3], multipliers = [3,2,1]
Output: 14
Explanation: The optimal solution is as follows: 
- Choose from the end, [1,2,3], adding 3 * 3 = 9 to the score.
- Choose from the end, [1,2], adding 2 * 2 = 4 to the score.
- Choose from the end, [1], adding 1 * 1 = 1 to the score.
The total score is 9 + 4 + 1 = 14.

Input: nums = [-5,-3,-3,-2,7,1], multipliers = [-10,-5,3,4,6]
Output: 102
Explanation: The optimal solution is as follows: 
- Choose from the start, [-5,-3,-3,-2,7,1], adding -5 * -10 = 50 to the score.
- Choose from the start, [-3,-3,-2,7,1], adding -3 * -5 = 15 to the score.
- Choose from the start, [-3,-2,7,1], adding -3 * 3 = -9 to the score.
- Choose from the end, [-2,7,1], adding 1 * 4 = 4 to the score.
- Choose from the end, [-2,7], adding 7 * 6 = 42 to the score. 
The total score is 50 + 15 - 9 + 4 + 42 = 102.

Solution#

Brute Force#

Based on problem description, at every i^th operation we have two choices of multiplication which are multipliers[i] * nums[left] and multipliers[i] * nums[right]. Each of the result will then be added to the multiplication of the rest of multipliers with either nums[left+1] or nums[right-1], hence the subproblems.

The subproblem, also called a state, indicates that we can use recursion to solve the problem. Each state is represented by:

1. left to indicate the left index to multiply by
2. right to indicate the right index to multiply by
3. op to indicate the number of the rest of operation

We could generate all possible states as follows:

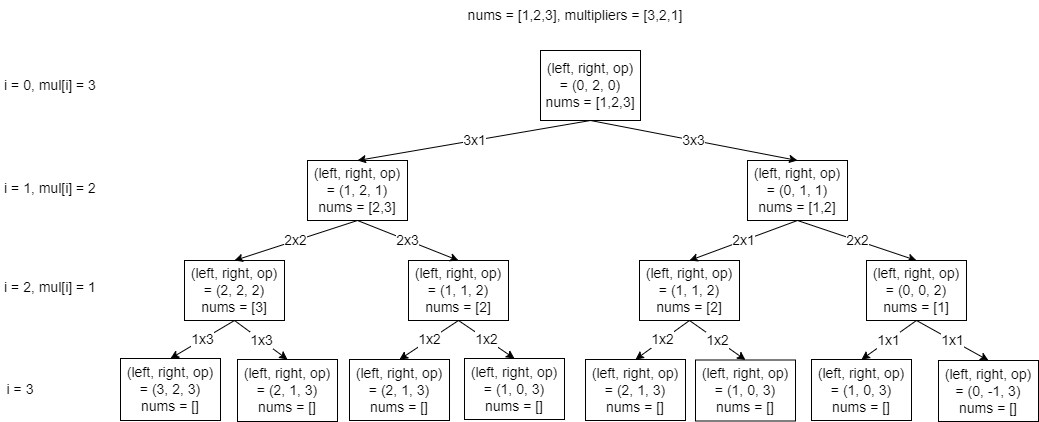
The algorithm is as follows:

1. Create an overload method of MaximumScore that takes three arguments: left, right and op
2. If op equals the length of multipliers which means we are done with all the operations, then it will return 0
3. Otherwise,
   • Multiply multipliers[op] with nums[left]. Then, solve the subproblem for the next operation op+1 with array nums range from left+1 to right. Add the result of the subproblem to the multiplication.
   • Multiply multipliers[op] with nums[right]. Then, solve the subproblem for the next operation op+1 with array nums range from left to right-1. Add the result of the subproblem to the multiplication.
4. Return the maximum of the two results
5. Create the initial call which means we have done 0 operation so far with array nums range from 0 to nums.Length - 1

• C#

public int MaximumScore(int[] nums, int[] multipliers)
{
    return MaximumScore(0, nums.Length - 1, 0);

    int MaximumScore(int left, int right, int op)
    {
        if (op == multipliers.Length)
            return 0;

        return Math.Max(multipliers[op] * nums[left] + MaximumScore(left + 1, right, op + 1),
                multipliers[op] * nums[right] + MaximumScore(left, right - 1, op + 1));
    }
}

Complexity Analysis#

Suppose M is the length of multipliers which is the same with the number of operations.

• Time Complexity: At each step we generate two subtree and the height of the tree is M. The total number of generated nodes is 2^M. Since, we traverse all the nodes, then the complexity will be O(2^M).
• Space Complexity: The complexity will be the same with O(recursion depth), thus it will be O(M).

Top-down Dynamic Programming#

Top-down Dynamic Programming approach can be viewed as the improvement of Brute Force approach. We can see from below image that there are some repeated states. These states should be memoized.

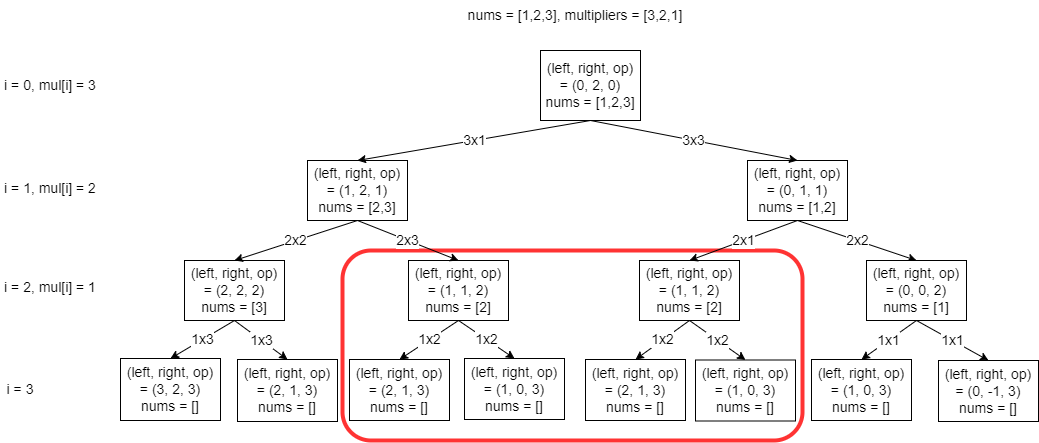
To formalize dynamic programming solution, we need to combine three things:

1. A function or data structure that answers the problem for a given state
   The function is MaximumScore(left, right, op) that denotes the maximum score we get after doing op operations on nums array ranges from left to right.
2. A recurrence relation that defines transition between states

   MaximumScore(left, right, op) = Max(
   multipliers[op] * nums[left] + MaximumScore(left + 1, right, op + 1), multipliers[op] * nums[right] + MaximumScore(left, right - 1, op + 1)
   )

3. Base cases
   MaximumScore(*, *, op) = 0 when op equals length of multipliers.

By memoizing the visited state, we can reduce the complexity.

• C#

public int MaximumScore(int[] nums, int[] multipliers)
{
    Dictionary<(int, int, int), int> memo = new Dictionary<(int, int, int), int>();
    return MaximumScore(0, nums.Length - 1, 0);

    int MaximumScore(int left, int right, int op)
    {
        if (op == multipliers.Length)
            return 0;

        if (!memo.TryGetValue((left, right, op), out var result))
        {
            result = Math.Max(multipliers[op] * nums[left] + MaximumScore(left + 1, right, op + 1),
                multipliers[op] * nums[right] + MaximumScore(left, right - 1, op + 1));

            memo.Add((left, right, op), result);
        }

        return result;
    }
}

Complexity Analysis#

Suppose M is the length of multipliers which is the same with the number of operations.

• Time Complexity: By memoizing the state, it will reduce the number of recursion call to the subproblems from 2^M to at most M² because at each state we have two calls that must be performed. Therefore, the complexity will be O(M²).
• Space Complexity: The memo will store at most M² number of state, thus the complexity will be O(M²).

Bottom-up Dynamic Programming#

Converting top-down to bottom-up technique is not straightforward. However, the rule of thumb is to use table or tabulation.

We can construct a table M+1 * M+1 where M is the length of multipliers. We use M+1 because we need placeholder to avoid IndexOutOfBoundsException.

Based on recursion tree in top-down approach, we work bottom up and compress the tree from the bottom in such way that it will fill only half of the table we provide.

• C#

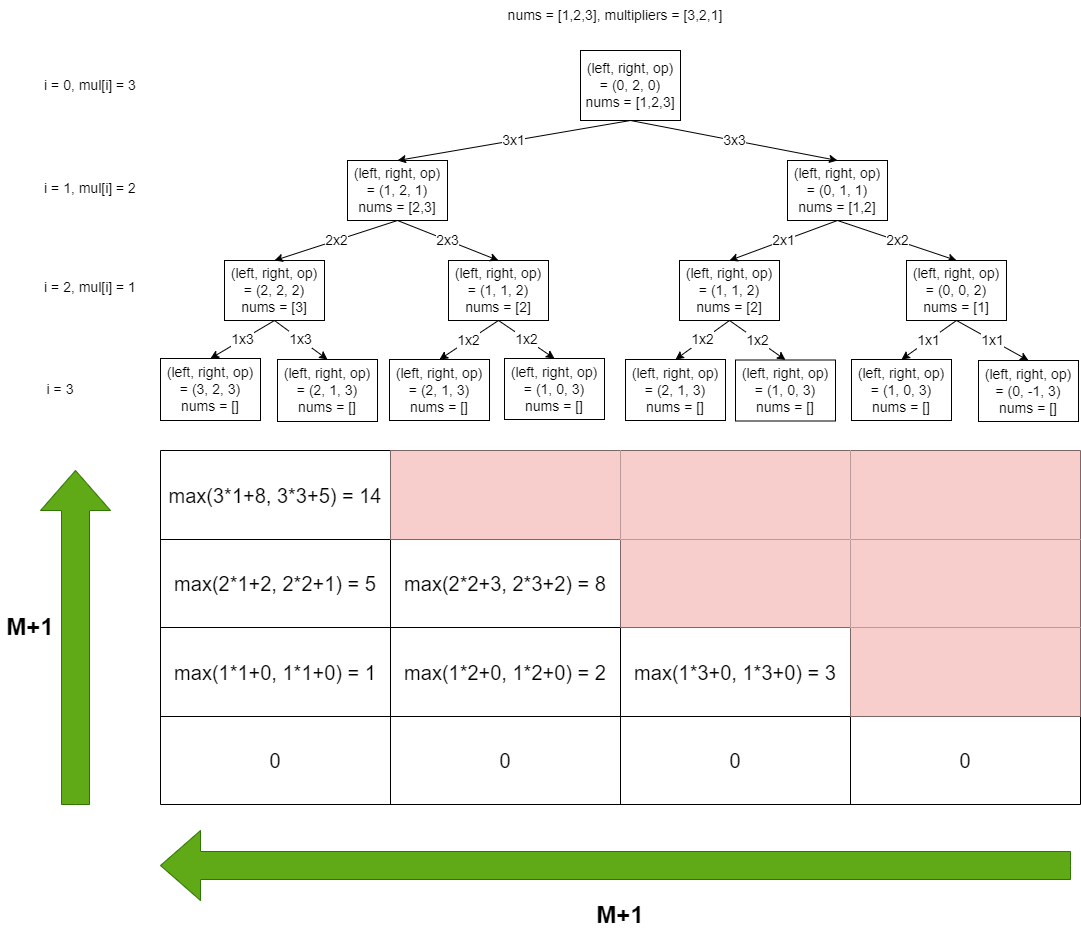
public int MaximumScore(int[] nums, int[] multipliers)
{
    int m = multipliers.Length;
    int n = nums.Length;
    int[,] dp = new int[m + 1, m + 1];

    for (int op = m - 1; op >= 0; op--)
    {
        for (int left = op; left >= 0; left--)
        {
            int right = n - 1 - (op - left);
            dp[op, left] = Math.Max(multipliers[op] * nums[left] + dp[op + 1, left + 1],
                multipliers[op] * nums[right] + dp[op + 1, left]);
        }
    }

    return dp[0, 0];
}

Complexity Analysis#

Suppose M is the length of multipliers.

• Time Complexity: Since the total of iteration is half of the matrix or M²/2, then the complexity is O(M²).
• Space Complexity: dp array has size (M+1)², thus the complexity is O(M²).