Trie Implementation in C#

Tagged: C#, Trie

Basic

Trie, sometimes also called Prefix Tree, is a data structure that stores every character of words in a Tree-style structure. The most popular application of Trie is Autocomplete system which is commonly found in search engine and IDE.

Trie consists of node that contains characters where if we traverse from the first character (root) to the leaf will form a word (string).

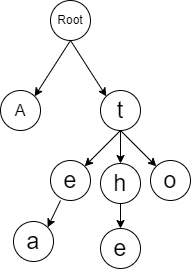
In below example, there are four words which are A,tea,the and to. A node (character) can have many children (characters). Each node also has IsEndOfWord property to mark whether the node is the end of a word (leaf) or not.

public class TrieNode
{
    public Dictionary<char, TrieNode> Children { get; set; }
    public bool IsEndOfWord { get; set; }

    public TrieNode()
    {
        Children = new Dictionary<char, TrieNode>();
        IsEndOfWord = false;
    }
}

public class Trie
{
    public TrieNode Root { get; }

    public Trie(TrieNode trieNode)
    {
        Root = trieNode;
    }

    // Code to insert a word

    // Code to search a word

    // Code to find words that start with specific prefix

    // Code to delete a word

    // Etc.
}

Implementation

Insertion

The algorithm to insert a word in a Trie:

Set root as current node
Iterating each character of the word
If children (dictionary) doesn’t contain the character, then add the character to current children
Get the node of current character and assign it to current node so that current node will point to the next character
Repeat step number 3 until finish iterating the word
Mark current node as a leaf by setting IsEndOfWord to be true

The complexity of this operation is O(n) where n is the length of the word.

public void Insert(string word)
{
    TrieNode current = Root;
    foreach (char ch in word)
    {
        if (!current.Children.ContainsKey(ch))
        {
            current.Children.Add(ch, new TrieNode());
        }
        current = current.Children[ch];
    }
    current.IsEndOfWord = true;
}

Deletion

To delete a word, we need to follow these steps:

Recursively traversing the Trie down to the leaf
If in the middle, current character is not in children, it means the word does not exist, we can return immediately
If we reach the end of the word but IsEndOfWord is not marked as the end of the word, it means it’s also not a valid word, we can return immediately.
Otherwise, we are now at the leaf. We can return and delete the leaf.

The complexity of this operation is O(n) where n is the length of the word.

public void Delete(string word)
{
    Delete(Root, word, 0);
}

private Boolean Delete(TrieNode current, string word, int index)
{
    if (index == word.Length)
    {
        if (!current.IsEndOfWord)
        {
            return false;
        }
        current.IsEndOfWord = false;
        return current.Children.Count == 0;
    }
    if (!current.Children.TryGetValue(word[index], out TrieNode node))
    {
        return false;
    }
    bool shouldDeleteCurrentNode = Delete(node, word, index + 1) && !node.IsEndOfWord;
    if (shouldDeleteCurrentNode)
    {
        current.Children.Remove(word[index]);
        return current.Children.Count == 0;
    }
    return false;
}

Searching

To search a word, we need to follow these steps:

Iterate each character of the word
If current node’s children do not contain the character, the word is not valid. We can return immediately. Otherwise, we should have reference to the next character’s node.
Set current node to refer to the next character’s node from previous step.
return IsEndOfWord to confirm whether we are on the leaf which means it is a word. Thus, we have found the word.

The complexity of this operation is O(n) where n is the length of the word.

public bool Search(string word)
{
    TrieNode current = Root;
    foreach (char ch in word)
    {
        if (!current.Children.TryGetValue(ch, out TrieNode node))
        {
            return false;
        }
        current = node;
    }

    return current.IsEndOfWord;
}

StartsWith

The implementation of StartsWith operation is the same with Search operation, except that in this operation we treat prefix as a word.

After we stop iteration, the last node will contain all nodes that will lead to all words that start with the prefix.

The complexity of StartsWith operation is O(n), but if we need to collect all the words, it will depend on the number of characters that we have after the prefix.

public List<string> StartsWith(string prefix)
{
    List<string> result = new List<string>();

    TrieNode current = Root;
    foreach (char ch in prefix)
    {
        if (!current.Children.TryGetValue(ch, out TrieNode node))
        {
            return result;
        }
        current = node;
    }
    
    StringBuilder sbPrefix = new StringBuilder(prefix);
    foreach (var pair in current.Children)
    {
        CreateStrings(sbPrefix.Append(pair.Key), pair, result);
        sbPrefix.Remove(sbPrefix.Length - 1, 1);
    }

    return result;
}

private void CreateStrings(StringBuilder prefix, KeyValuePair<char, TrieNode> pair, List<string> result)
{
    if (pair.Value.Children.Count == 0)
    {
        result.Add(prefix.ToString());
        return;
    }

    foreach (var child in pair.Value.Children)
    {
        CreateStrings(prefix.Append(child.Key), child, result);
        prefix.Remove(prefix.Length - 1, 1);
    }
}

Trie Implementation in C#

Basic#

Implementation#

Insertion#

Deletion#

Searching#

StartsWith#

Basic

Implementation

Insertion

Deletion

Searching

StartsWith