Top K Frequent Elements

Tagged: Array, Hash Table, Divide and Conquer, Sorting, Priority Queue, Heap, Bucket Sort, Counting, Quickselect

Problem

Given an array of integer and integer K, our task is to find the K most frequent elements in the Array. The K most frequent elements can be in any order.

For example,

Input: nums = [2,2,3,1,1,1], k = 2
Output: [1,2]
Explanation: The 2 most frequent elements are [1,2]. [2,1] is also a valid output because the output doesn't have to be sorted.

Input: nums = [1], k = 1
Output: 1
Explanation: The 1 most frequent elements is only 1.

Solution

Priority Queue (Heap)

The problem sugggests us to track the frequency of every number appears in the array nums. The most suitable data structure to store this information is map where it will associate every number with its frequency.

The algorithm works as follows:

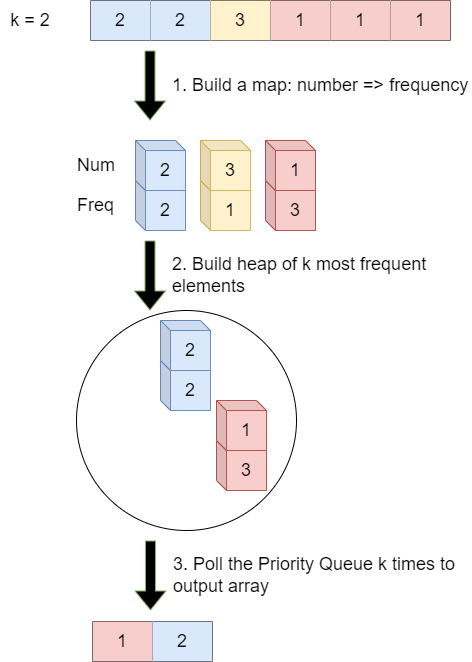
Create frequency table that maps each unique number to its frequency. For example, when the input is [2,2,3,1,1,1], then the map will be {2->2, 3->1, 1->3}.
Enqueue all entries in the map to Priority Queue. Whenever the size of the queue exceed k, we will dequeue so that eventually the queue will contains only k elements.
Iterate k times to dequeue the element and store it into the output array.

public int[] TopKFrequent(int[] nums, int k)
{
    Dictionary<int, int> freqMap = new Dictionary<int, int>();
    foreach (int num in nums)
    {
        freqMap[num] = freqMap.GetValueOrDefault(num, 0) + 1;
    }

    PriorityQueue<int, int> heap = new PriorityQueue<int, int>(
        Comparer<int>.Create((x, y) => x - y)
    );
    foreach (var freqEntry in freqMap)
    {
        heap.Enqueue(freqEntry.Key, freqEntry.Value);
        if (heap.Count > k)
            heap.Dequeue();
    }

    int[] result = new int[k];
    for (int i = k - 1; i >= 0; i--)
    {
        result[i] = heap.Dequeue();
    }

    return result;
}

fun topKFrequent(nums: IntArray, k: Int): IntArray {
    val map = mutableMapOf<Int, Int>()
    nums.forEach {
        map[it] = map.getOrDefault(it, 0) + 1
    }

    val priorityQueue = PriorityQueue<Pair<Int, Int>>(
        compareByDescending { it.second }
    )
    map.forEach {
        priorityQueue.add(Pair(first = it.key, second = it.value))
    }

    val result = IntArray(k)
    var i = 0
    while (i < k && priorityQueue.isNotEmpty()) {
        result[i] = priorityQueue.remove().first
        i++
    }

    return result
}

class ElementFrequency {
    private int element;
    private int frequency;

    public ElementFrequency(int element, int frequency) {
        this.element = element;
        this.frequency = frequency;
    }

    public int getFrequency() {
        return this.frequency;
    }
}

public int[] topKFrequent(int[] nums, int k) {
    Map<Integer, Integer> map = new HashMap<>();
    for (int num : nums) {
        map.put(num, map.getOrDefault(num, 0) + 1);
    }

    PriorityQueue<ElementFrequency> priorityQueue = new PriorityQueue<>(
            Comparator.comparing(ElementFrequency::getFrequency).reversed()
    );
    map.forEach((key, value) -> {
                priorityQueue.add(new ElementFrequency(key, value));
            }
    );

    int[] result = new int[k];
    int i = 0;
    while (i < k && !priorityQueue.isEmpty()) {
        result[i] = priorityQueue.remove().element;
        i++;
    }

    return result;      
}

Complexity Analysis

Suppose N is the length of array nums.

Time Complexity: The first step to build frequency map has O(N) complexity, then the second step builds heap with size k using N elements will have O(N log k) complexity. The last step has O(k) complexity. Since the second step is the dominant part of the algorithm, then the overall complexity is O(N log k).
Space Complexity: O(N + k) since building frequency map requires N spaces and the priority queue requires k spaces.

Quickselect

Quickselect can be seen as partially applying Quicksort algorithm in order to get the most k frequent elements. Therefore, the algorithm will be similar to Quicksort.

The algorithm works as follows:

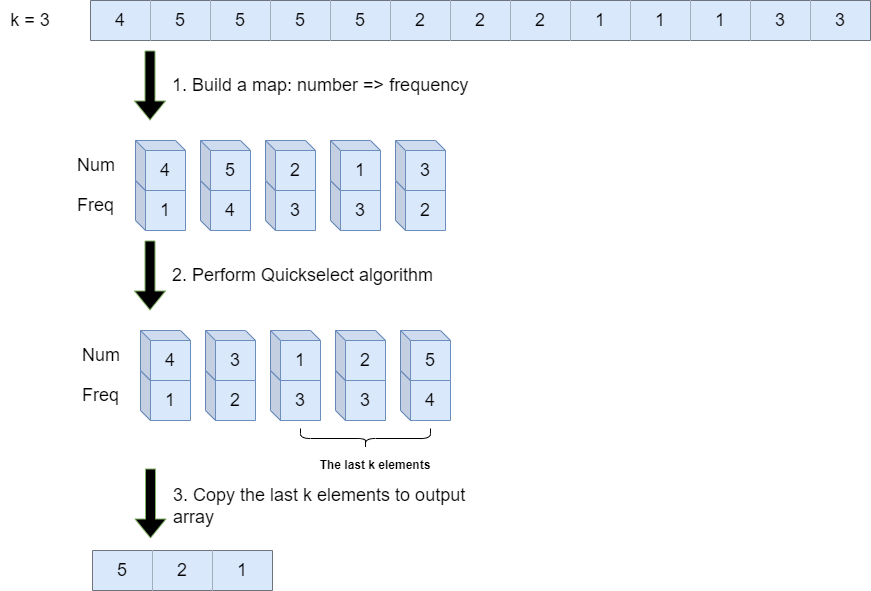
Create frequency table that maps each unique number to its frequency. For example, when the input is [2,2,3,1,1,1], then the map will be {2->2, 3->1, 1->3}.
Perform Quickselect algorithm which is similar to Quicksort. So, instead of fully sorted the array, we only need to perform quicksort with focus only on the right side where the last k elements reside. It also doesn’t have to be sorted. Here we use Hoare Partition Algorithm that works well with repeated elements.
Iterate k times to copy the last k elements into the output array.

public int[] TopKFrequent(int[] nums, int k)
{
    Dictionary<int, int> freqMap = new Dictionary<int, int>();
    foreach (int num in nums)
    {
        freqMap[num] = freqMap.GetValueOrDefault(num, 0) + 1;
    }

    int[][] freqArray = new int[freqMap.Count][];
    int i = 0;
    foreach (var freqEntry in freqMap)
    {
        freqArray[i] = new int[2];
        freqArray[i][0] = freqEntry.Key;
        freqArray[i][1] = freqEntry.Value;

        i++;
    }

    QuickSelect(freqArray, freqArray.Length - k, 0, freqArray.Length - 1);

    int[] result = new int[k];
    i = 0;
    while (i < k)
    {
        result[i] = freqArray[freqArray.Length - 1 - i][0];
        i++;
    }

    return result;
}

private void QuickSelect(int[][] freqArray, int k, int low, int high)
{
    if (low == high)
        return;

    int position = HoarePartition(freqArray, low, high);
    if (k <= position)
        QuickSelect(freqArray, k, low, position);
    else
        QuickSelect(freqArray, k, position + 1, high);
}

private int HoarePartition(int[][] freqArray, int low, int high)
{
    int mid = low + (high - low) / 2;
    int pivot = freqArray[mid][1];

    int left = low - 1;
    int right = high + 1;
    while (true)
    {
        do
        {
            left++;
        } while (freqArray[left][1] < pivot);
        do
        {
            right--;
        } while (freqArray[right][1] > pivot);

        if (left >= right) return right;

        int[] temp = freqArray[left];
        freqArray[left] = freqArray[right];
        freqArray[right] = temp;
    }
}

fun topKFrequent(nums: IntArray, k: Int): IntArray {
    val map = mutableMapOf<Int, Int>()
    nums.forEach {
        map[it] = map.getOrDefault(it, 0) + 1
    }

    val arr = Array<Pair<Int, Int>>(map.size) { Pair(first = 0, second = 0) }
    var i = 0
    map.forEach {
        arr[i] = Pair(first = it.key, second = it.value)
        i++
    }

    quickSelect(arr, map.size - k, 0, map.size - 1)
    val result = IntArray(k)
    i = 0
    while (i < k) {
        result[i] = arr[arr.size - 1 - i].first
        i++
    }
    return result
}

private fun quickSelect(nums: Array<Pair<Int, Int>>, k: Int, low: Int, high: Int) {
    if (low == high) return

    val position: Int = hoarePartition(nums, low, high)
    return if (k <= position) quickSelect(nums, k, low, position) else quickSelect(nums, k, position + 1, high)
}

private fun hoarePartition(nums: Array<Pair<Int, Int>>, low: Int, high: Int): Int {
    val pivot = nums[(low + high) / 2].second

    var i = low - 1
    var j = high + 1
    while (true) {
        do {
            i++
        } while (nums[i].second < pivot)
        do {
            j--
        } while (nums[j].second > pivot)

        if (i >= j) return j

        nums[i] = nums[j].also {
            nums[j] = nums[i]
        }
    }
}

class ElementFrequency {
    private int element;
    private int frequency;

    public ElementFrequency(int element, int frequency) {
        this.element = element;
        this.frequency = frequency;
    }

    public int getFrequency() {
        return this.frequency;
    }
}

public int[] topKFrequent(int[] nums, int k) {
    Map<Integer, Integer> map = new HashMap<>();
    for (int num : nums) {
        map.put(num, map.getOrDefault(num, 0) + 1);
    }

    ElementFrequency[] arr = new ElementFrequency[map.size()];
    int i = 0;
    for (Integer key : map.keySet()) {
        arr[i] = new ElementFrequency(key, map.get(key));
        i++;
    }

    quickSelect(arr, map.size() - k, 0, map.size() - 1);
    int[] result = new int[k];
    i = 0;
    while (i < k) {
        result[i] = arr[arr.length - 1 - i].element;
        i++;
    }

    return result;
}

private void quickSelect(ElementFrequency[] nums, int k, int low, int high) {
    if (low == high) return;

    int position = hoarePartition(nums, low, high);
    if (k <= position)
        quickSelect(nums, k, low, position);
    else
        quickSelect(nums, k, position + 1, high);
}

private int hoarePartition(ElementFrequency[] nums, int low, int high) {
    int pivot = nums[(low + high) / 2].frequency;

    int i = low - 1;
    int j = high + 1;
    while (true) {
        do {
            i++;
        } while (nums[i].frequency < pivot);
        do {
            j--;
        } while (nums[j].frequency > pivot);

        if (i >= j) return j;

        ElementFrequency temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

Complexity Analysis

Suppose N is the length of array nums.

Time Complexity: The first step to build frequency map has O(N) complexity, then QuickSelect algorithm that only partially sorts k last elements of unique array will have O(N log k) complexity. The last step to copy elements to output array has O(k) complexity. Since the second step is the dominant part of the algorithm, then the overall complexity is O(N log k).
Space Complexity: O(N) since building frequency map requires N spaces and the second step to store array of unique element requires maximum N spaces in case all elements are unique.

Bucket Sort

Bucket Sort can also be used to solve this problem. It has overall better complexity compared to previous algorithms.

The algorithm works as follows:

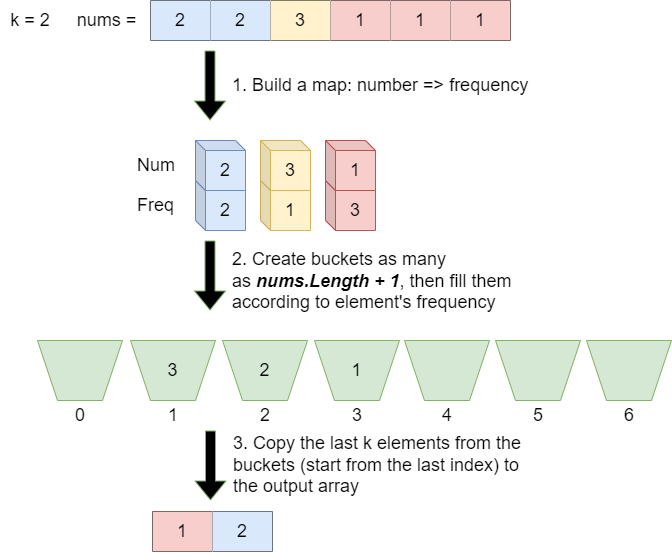
Create frequency table that maps each unique number to its frequency. For example, when the input is [2,2,3,1,1,1], then the map will be {2->2, 3->1, 1->3}.
Create buckets as many as nums.Length + 1, then fill the buckets according to element’s frequency. Bucket’s index represents frequency number. We provide nums.Length + 1 buckets because for the edge case where the array only contains one element, thus the element must be placed at bucket number nums.Length or the last bucket. Otherwise, the index will be out of bounds.
Copy the last k elements from the buckets (start from the last index of the buckets) to the output array.

public int[] TopKFrequent(int[] nums, int k)
{
    Dictionary<int, int> frequencyMap = new Dictionary<int, int>();
    foreach (int num in nums)
    {
        frequencyMap[num] = frequencyMap.GetValueOrDefault(num, 0) + 1;
    }

    List<int>[] buckets = new List<int>[nums.Length + 1];
    foreach (var frequencyEntry in frequencyMap)
    {
        int frequency = frequencyEntry.Value;
        if (buckets[frequency] == null)
        {
            buckets[frequency] = new List<int>();
        }
        buckets[frequency].Add(frequencyEntry.Key);
    }

    int[] result = new int[k];
    for (int i = buckets.Length - 1; k > 0; i--)
    {
        if (buckets[i] != null)
        {
            foreach (int num in buckets[i])
            {
                k -= 1;
                result[k] = num;
                if (k == 0)
                {
                    break;
                }
            }
        }
    }

    return result;
}

fun topKFrequent(nums: IntArray, k: Int): IntArray {
    var min = nums[0]
    var max = nums[0]
    for (num in nums) {
        if (num > max) max = num else if (num < min) min = num
    }

    val frequencies = IntArray(max - min + 1)
    for (num in nums) {
        frequencies[num - min]++
    }

    val buckets = arrayOfNulls<ArrayList<Int>>(nums.size + 1)
    for (i in frequencies.indices) {
        val num = i + min
        val frequency = frequencies[i]
        if (buckets[frequency] == null) {
            buckets[frequency] = ArrayList()
        }
        buckets[frequency]!!.add(num)
    }

    var k = k
    val result = IntArray(k)
    var i = buckets.size - 1
    while (k > 0) {
        buckets[i]?.let {
            for (num in buckets[i]!!) {
                k -= 1;
                result[k] = num;
                if (k == 0) {
                    break;
                }
            }
        }
        i--
    }

    return result
}

public int[] topKFrequent(int[] nums, int k) {
    int min = nums[0], max = nums[0];
    for (int num : nums) {
        if (num > max)
            max = num;
        else if (num < min)
            min = num;
    }

    int[] frequencies = new int[max - min + 1];
    for (int num : nums) {
        frequencies[num - min]++;
    }

    List<Integer>[] buckets = new List[nums.length + 1];
    for (int i = 0; i < frequencies.length; i++) {
        int num = i + min;
        int frequency = frequencies[i];
        if (buckets[frequency] == null) {
            buckets[frequency] = new ArrayList<>();
        }
        buckets[frequency].add(num);
    }

    int[] result = new int[k];
    for (int i = buckets.length - 1; k > 0; i--) {
        if (buckets[i] != null) {
            for (int num : buckets[i]) {
                k -= 1;
                result[k] = num;
                if (k == 0) {
                    break;
                }
            }
        }
    }

    return result;     
}

Complexity Analysis

Suppose N is the length of array nums.

Time Complexity: Since we iterate linearly in every steps of algorithm, then the complexity is O(N).
Space Complexity: Since the collection that we use requires maximum N+1 space, then the complexity is O(N).

Top K Frequent Elements

Problem#

Solution#

Priority Queue (Heap)#

Complexity Analysis#

Quickselect#

Complexity Analysis#

Bucket Sort#

Complexity Analysis#

Problem

Solution

Priority Queue (Heap)

Complexity Analysis

Quickselect

Complexity Analysis

Bucket Sort

Complexity Analysis