Longest Palindromic Substring

Tagged: String, Dynamic Programming, Two Pointers

Problem#

Given a string, our task is to find the longest palindromic substring in that string.
For example,

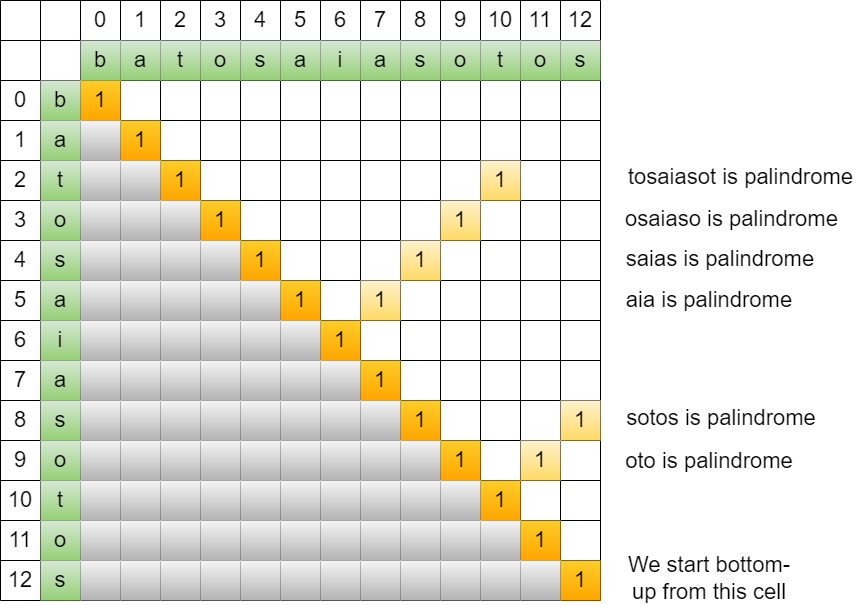
Input: s = "batosaiasotos"
Output: "tosaiasot"
Explanation: There are many palindrome strings which are "tosaiasot", "osaiaso", "saias", "sotos", etc.
But the longest one is "tosaiasot".

Solution#

Dynamic Programming#

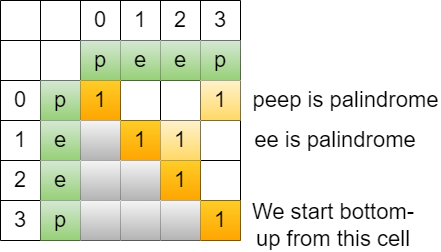
A two-dimensional array is created to mark the start and the end of palindromic substring. We will work bottom-up to find all palindromic substrings.

By default, each character (length 1) is a palindromic substring. Therefore, initially we will mark table’s diagonal cell as true which represents each character index (location). This will also become the start of palindromic substring of length greater than one.

We also know that the substring from i to j is palindrome if substring from i+1 to j-1 is also a palindrome, i.e. dp[i][j] is true if dp[i+1][j-1] is also true. Besides that, two adjacent characters that are the same is also a palindrome.

With above information, as we work bottom-up, we will find all palindromic substrings and its length. In the meantime, we can compare each of the length we got with the longest we got so far, thus we will get the longest palindromic substring.

• C#

public string LongestPalindrome(string s)
{
    int longest = 1;
    int startIndex = 0;

    bool[,] dp = new bool[s.Length, s.Length];
    for (int i = 0; i < s.Length; i++)
    {
        dp[i, i] = true;
    }

    for (int i = s.Length - 1; i >= 0; i--)
    {
        for (int j = i + 1; j < s.Length; j++)
        {
            if (s[i] == s[j])
            {
                if (j - i == 1 || dp[i + 1, j - 1])
                {
                    dp[i, j] = true;
                }
            }

            if (dp[i, j] && j - i + 1 > longest)
            {
                longest = j - i + 1;
                startIndex = i;
            }
        }
    }

    return s.Substring(startIndex, longest);
}

Two Pointers - Expand Around Center#

There are two possibilities regarding the center of palindrome:

1. It consists of 1 character, e.g., aba
2. It consists of 2 characters, e.g., abba

At every index of String s, we will try to expand to the left and right of the center using two pointers technique.

The illustration is as follows.

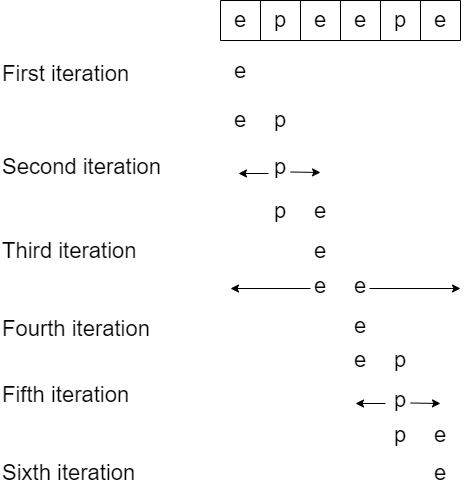
In the first iteration above, we don’t get any palindrome.

However, in the second iteration we get one palindrome epe whose length is 3 and the center of palindrome consists of one character. It’s the same with fifth iteration.

In the third iteration, we get the longest palindromic substring which has length 6, that is epeepe. The center of this palindrome consists of two characters.

The example above shows that we need to check two possibilies of palindrome with regards to its center at every index of the string s.

• C#

public string LongestPalindrome(string s)
{
    int start = 0;
    int longest = 0;
    for (int i = 0; i < s.Length; i++)
    {
        int len1 = ExpandAroundCenter(s, i, i);
        int len2 = ExpandAroundCenter(s, i, i + 1);
        int len = Math.Max(len1, len2);
        if (len > longest)
        {
            start = i - (len - 1) / 2;
            longest = len;
        }
    }

    return s.Substring(start, longest);
}

private int ExpandAroundCenter(string s, int left, int right)
{
    while (left >= 0 && right < s.Length && s[left] == s[right])
    {
        left--;
        right++;
    }

    return right - left - 1;
}