Intersection of Two Linked Lists

Tagged: Brute Force, Hash Table, Linked List, Two Pointers

Problem

This problem states that given the head of two singly linked lists, our task is to find the node where the two linked lists start to intersect.
Below are the examples: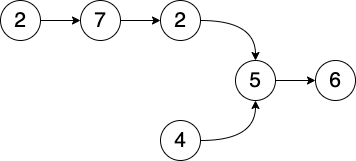

Input: listA = [2,7,2,5,6], listB = [4,5,6]
Output: Node 5
Explanation: The two linked lists start to intersect at node 5

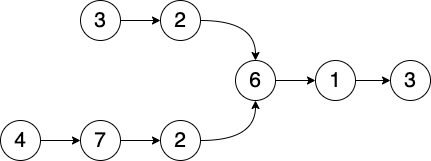
Input: listA = [3,2,6,1,3], listB = [4,7,2,6,1,3]
Output: Node 6
Explanation: The two linked lists start to intersect at node 6

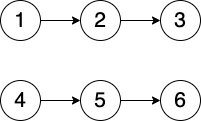
Input: listA = [1,2,3], listB = [4,5,6]
Output: null
Explanation: There is no intersection between the two linked lists

Note: Please remember, in order to find the intersection, we have to use node comparison

Solution

Below is a singly linked list code that will be used in the solution.

public class ListNode
{
    public int val;
    public ListNode next;

    public ListNode(int x)
    {
        val = x;
    }
}

public class SinglyLinkedList
{
    public ListNode headNode;

    public void InsertLast(ListNode newNode)
    {
        if (headNode == null)
        {
            headNode = newNode;
        }
        else
        {
            ListNode temp = headNode;

            while (temp.next != null)
            {
                temp = temp.next;
            }

            temp.next = newNode;
        }
    }
}

Brute Force

This is a naive and the least efficient algorithm. The intuition is simple. We start comparing each node from linked list A then iterating through linked list B to compare whether the node A equals with node B. If equals then it must be the intersection node. Here, we compare two list node object not the value inside the node.

public ListNode GetIntersectionNode(ListNode headA, ListNode headB)
{
    while (headA != null)
    {
        ListNode tempB = headB;
        while (tempB != null)
        {
            if (headA == tempB)
                return headA;
            tempB = tempB.next;
        }

        headA = headA.next;
    }

    return null;
}

Time Complexity: Suppose linked list A and B have length N and M respectively. Then, linked list B will be iterated M times while it will be reiterated as much as N times. Therefore, the time complexity is O(M x N).
M + M + M + … + M = M x N
Space Complexity: The space complexity is O(1) because we don’t use any storage that will grow with the size of the input.

Hash Table

Previous algorithm is inefficient because we have to constantly iterate linked list B to check whether every node A presents in linked list B. If we can replace the checking part with other method that requires constant time then it would be more efficient.
Hash Table is a suitable data structure in this case since the lookup process has O(1) complexity. Therefore, to utilize Hash Table, we need to store each element of linked list B to hash table or similar data structure. In this case, we will use Set since we only need the key not key value as in hash table and the key will be every node B.
After that, we only need to traverse linked list A then check whether the set contains node A. If yes, then it must be the intersection node. If none, then there is no intersection between the two linked lists.
One thing to remember is we compare the node object and not the value inside the node because two objects can have the same value inside.

public ListNode GetIntersectionNode(ListNode headA, ListNode headB)
{
    HashSet<ListNode> setsB = new HashSet<ListNode>();

    ListNode tempB = headB;
    while (tempB != null)
    {
        setsB.Add(tempB);

        tempB = tempB.next;
    }

    ListNode tempA = headA;
    while (tempA != null)
    {
        if (setsB.Contains(tempA))
        {
            return tempA;
        }

        tempA = tempA.next;
    }

    return null;
}

Time Complexity: In this algorithm, we traverse linked list A and B separately. First we need to traverse linked list B M times. Then, we traverse linked list A N times. Combining these two iterations, we will get M+N iterations in total. Therefore, the time complexity is O(M + N).
Space Complexity: The space complexity is O(M) because we need hash table to store M elements of linked list B that will be used for lookup.
Alternatively, we can store element of linked list A to Hash Table, but in general there is no real difference unless the length difference is very significant.

Two Pointers with Three Loops

public ListNode GetIntersectionNode(ListNode headA, ListNode headB)
{
    int sizeA = GetSize(headA);
    int sizeB = GetSize(headB);

    for (int i = 0; i < Math.Abs(sizeA - sizeB); i++)
    {
        if (sizeA > sizeB)
        {
            headA = headA.next;
        }
        else
        {
            headB = headB.next;
        }
    }

    while (headA != null && headB != null)
    {
        if (headA == headB)
        {
            return headA;
        }

        headA = headA.next;
        headB = headB.next;
    }

    return null;
}

private int GetSize(ListNode head)
{
    ListNode pointer = head;
    int count = 0;

    while (pointer != null)
    {
        count++;
        pointer = pointer.next;
    }

    return count;
}

Two Pointers with Single Loop

public ListNode GetIntersectionNode(ListNode headA, ListNode headB)
{
    ListNode pointerA = headA;
    ListNode pointerB = headB;
    while (pointerA != pointerB) {
        pointerA = pointerA == null ? headB : pointerA.next;
        pointerB = pointerB == null ? headA : pointerB.next;
    }
    return pointerA;
}

Intersection of Two Linked Lists

Problem#

Solution#

Brute Force#

Hash Table#

Two Pointers with Three Loops#

Two Pointers with Single Loop#