How to Detect Cycle in a Linked List

Tagged: Algorithms, Linked List, C#

Problem#

Suppose you are given a Singly Linked List where the tail’s pointer points to a node within the list such that it will create a cycle/loop if the list is traversed continuously, how do you detect such a cycle exists?

Below are some of the examples:

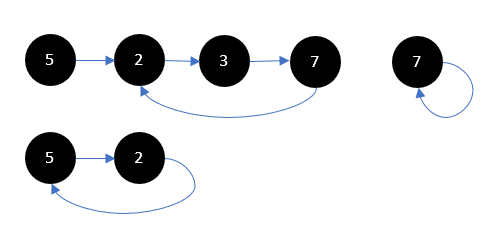
This tutorial will show you some algorithms that can be used to solve this problem. Our ultimate goal is to achieve Time Complexity O(n) and Space Complexity O(1).

Solution#

Hash Table / Dictionary / HashSet#

public static bool HasCycle(ListNode head)
{
    HashSet<ListNode> listNodes = new HashSet<ListNode>();
    while (head != null)
    {
        if (listNodes.Contains(head))
        {
            return true;
        }
        listNodes.Add(head);
        head = head.next;
    }
    return false;
}

This algorithm traverses through the list and stores ListNode object into HashSet data structure. If the set contains the node already, it means the Linked List contains a cycle.

Time Complexity O(n) and Space Complexity O(n).

Floyd’s Cycle Finding Algorithm#

public static bool HasCycle(ListNode head)
{
    if (head == null || head.next == null)
        return false;

    ListNode tortoise = head;
    ListNode hare = head.next;
    while (tortoise != hare)
    {
        if (hare == null || hare.next == null)
            return false;

        tortoise = tortoise.next;
        hare = hare.next.next;
    }

    return true;
}

This algorithm is based on two-pointer algorithm where there are two pointer named Tortoise and Hare. Tortoise is the slow runner while Hare is the faster one.

At the beginning Hare is one step ahead, but later Hare will have two steps at a time while Tortoise will have only one step at a time. With this condition, Hare will enter the loop first and eventually will catch up Tortoise inside the loop which means there is a cycle inside the Linked List.

Time Complexity O(n) and Space Complexity O(1).