Delete and Earn

Tagged: Array, Hash Table, Dynamic Programming

Problem#

Given an array of integer nums. Our task is to maximize the number of points we can get by following below operation any number of times:

• Pick any nums[i] and delete it to earn nums[i] points. Afterwards, you must delete every element equal to nums[i] - 1 and every element equal to nums[i] + 1.

Return the maximum number of points we can earn by applying the above operation some number of times.

For example,

Input: nums = [3,4,2]
Output: 6
Explanation: You can perform the following operations:
- Delete 4 to earn 4 points. Consequently, 3 is also deleted. nums = [2].
- Delete 2 to earn 2 points. nums = [].
You earn a total of 6 points.

Input: nums = [2,2,3,3,3,4]
Output: 9
Explanation: You can perform the following operations:
- Delete a 3 to earn 3 points. All 2's and 4's are also deleted. nums = [3,3].
- Delete a 3 again to earn 3 points. nums = [3].
- Delete a 3 once more to earn 3 points. nums = [].
You earn a total of 9 points.

Constraints:

• 1 <= nums.length <= 2 * 104
• 1 <= nums[i] <= 104

Solution#

In the description there is a phrase you must delete every element equal.... To simplify operating with every element at once, the most logical data structure is map that can be implemented as Dictionary in C# or HashMap in Java.

This will form our preprocessing step as illustrated in image below.

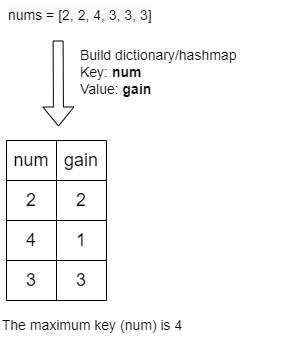
With input nums = [2, 2, 4, 3, 3, 3], it might be tempting to sort map by the key. However, we don’t need it since we are going to work with index ranging from 0 to the maximum number of the key which is 4 in this case.

Similar to previous House Robber problem, we could determine current state based on previous states. At any point (num) we have two choices:

• Compute total points (gain) for current number plus maximum number of points we get from previous two number, i.e., DeleteAndEarn(maxNumber - 2) or
• Compute maximum number of points we get from previous number, i.e., DeleteAndEarn(maxNumber - 1)

To summarize:

DeleteAndEarn(maxNumber) = Math.Max(DeleteAndEarn(maxNumber - 1), DeleteAndEarn(maxNumber - 2) + gain)

where gain is total points we earn from current number. If current number doesn’t exist in the map, it will return 0.

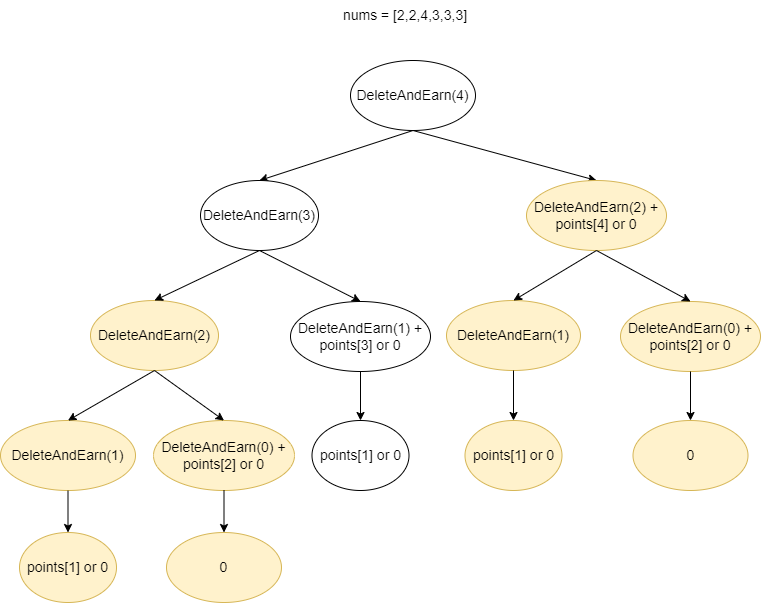
This will lead us to our first solution (Brute Force) before we perform any optimization.

Brute Force#

• C#

public int DeleteAndEarn(int[] nums)
{
    int maxNumber = 0;
    Dictionary<int, int> points = new Dictionary<int, int>();

    foreach (int num in nums)
    {
        points[num] = points.GetValueOrDefault(num, 0) + num;
        maxNumber = Math.Max(maxNumber, num);
    }

    return DeleteAndEarn(maxNumber);

    int DeleteAndEarn(int maxNumber)
    {
        if (maxNumber == 0)
            return 0;

        if (maxNumber == 1)
            return points.GetValueOrDefault(1, 0);

        int gain = points.GetValueOrDefault(maxNumber, 0);
        return Math.Max(DeleteAndEarn(maxNumber - 1), DeleteAndEarn(maxNumber - 2) + gain);
    }
}

Complexity Analysis#

Suppose N is the maximum number in nums.

• Time Complexity: At each step we generate two subtree and the height of the tree is N. The total number of generated nodes is 2^N. Since, we traverse all the nodes, then the complexity will be O(2^N).
• Space Complexity: The complexity will be the same with O(recursion depth), thus it will be O(N).

Top-down Dynamic Programming#

• C#

public int DeleteAndEarn(int[] nums)
{
    int maxNumber = 0;
    Dictionary<int, int> points = new Dictionary<int, int>();

    foreach (int num in nums)
    {
        points[num] = points.GetValueOrDefault(num, 0) + num;
        maxNumber = Math.Max(maxNumber, num);
    }

    int[] maxPoints = new int[maxNumber + 1];

    return DeleteAndEarn(maxNumber);

    int DeleteAndEarn(int maxNumber)
    {
        if (maxNumber == 0)
            return 0;

        if (maxNumber == 1)
            return points.GetValueOrDefault(1, 0);

        if (maxPoints[maxNumber] > 0)
            return maxPoints[maxNumber];

        int gain = points.GetValueOrDefault(maxNumber, 0);
        maxPoints[maxNumber] = Math.Max(DeleteAndEarn(maxNumber - 1), DeleteAndEarn(maxNumber - 2) + gain);

        return maxPoints[maxNumber];
    }
}

Complexity Analysis#

Suppose N is the maximum number in nums.

• Time Complexity: Since we cache each DeleteAndEarn(i), then we will perform at most N recursive calls, thus the complexity is O(N).
• Space Complexity: The complexity will be the same with O(recursion depth), thus it will be O(N).

Bottom-up Dynamic Programming#

This approach is the most efficient since we can avoid recursion stack overhead by using for-loop iteration linearly.

The solution is also similar to previous House Robber Bottom Up Dynamic Programming solution.

The algorithm works as follows:

1. We provide maxPoints array to cache the result of every state
2. Initialize maxPoints for 0 and 1
3. Then linearly we will compute maxPoints for every number from 2 to the maximum number in nums based on our preprocessing step. The result will be stored in maxPoints cache where it can be reused to compute future state, i.e.,

   maxPoints[num] = Math.Max(maxPoints[num - 1], maxPoints[num - 2] + gain).

• C#

public int DeleteAndEarn(int[] nums)
{
    int maxNumber = 0;
    Dictionary<int, int> points = new Dictionary<int, int>();

    foreach (int num in nums)
    {
        points[num] = points.GetValueOrDefault(num, 0) + num;
        maxNumber = Math.Max(maxNumber, num);
    }

    int[] maxPoints = new int[maxNumber + 1];
    maxPoints[0] = 0;
    maxPoints[1] = points.GetValueOrDefault(1, 0);

    for (int num = 2; num < maxPoints.Length; num++)
    {
        int gain = points.GetValueOrDefault(num, 0);
        maxPoints[num] = Math.Max(maxPoints[num - 1], maxPoints[num - 2] + gain);
    }

    return maxPoints[maxNumber];
}

Complexity Analysis#

Suppose N is the maximum number in nums.

• Time Complexity: Since we iterate linearly up to N, then the complexity is O(N).
• Space Complexity: O(N) since we allocate memory as many as N+1 to array maxPoints for caching.